“滤波器救世主”能带来完美的声音复制吗?
近期最流行的技术是有限脉冲响应(FIR)的滤波器。如同音频系统中已经存在了很长时间的概念性技术一样,直到今天科技的发展才使它们具备实际应用性。这是我们一直在等待的灵丹妙药吗?“滤波器救世主”最终能带来完美的声音复制吗?
当然不能
但它们还是非常酷的,
能够改变某些应用的游戏规则。
这是系列文章的第1部分,用于检视FIR滤波器在扩声系统中的使用。网上有大量深入研究数学运算和深层理论的教程和资源,不过FIR滤波器理论知识就像一个无底深井,永远也讲不完。在本系列中,我将结合一些“实例”以及实际操作和示例,大致讲解FIR滤波器理论。这有助于了解FIR和将FIR滤波技术整合到项目中。
在此,读者需要对基础信号理论有一定的了解,包括现代音频和声学信号分析仪在进行信号分析时涉及的时域和频域概念。
什么是FIR滤波器?
理解FIR滤波器的其中一种方法是将其与相对应的无限脉冲响应(IIR)滤波器进行比较。一般来说,IIR可以是模拟或与模拟滤波器行为特征相似的数字滤波器。IIR通过使用“好的”反馈将一部分输出信号返回到输入端进行再处理。
这种“递归”行为意味着,滤波器的脉冲响应(理论上)永远不会衰减到零。当然,实际上这类滤波器的脉冲响应最终仍然会衰减至零,因为输出信号最终会降低到本底噪音。由于它们使用了反馈信号,若设计不当,IIR滤波器的工作状态可能不稳定。所有模拟滤波器都是IIR滤波器。
假设我们使用模拟或IIR参数均衡器来创建扬声器均衡曲线(图1和图2)。 其中包括一个高通、一个低通,以及在通带内进行一些提升和衰减。
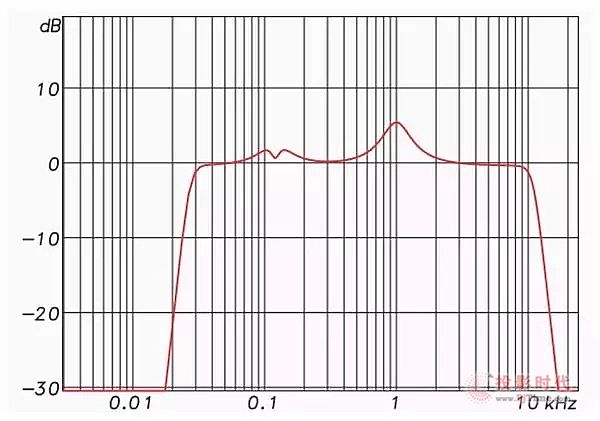
图1:均衡器的频率响应幅度
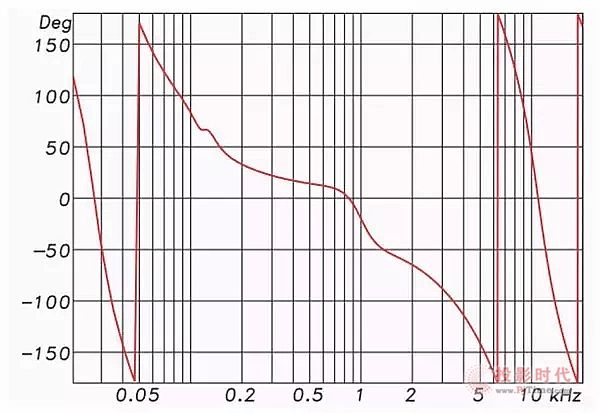
图2:均衡器的频率相位响应
响应中的每个“凸起”表示在该频率的相移(负向相位角),并且每个“下降”表示在该频率的反向相移(正向相位)。高通和低通滤波器都会导致负向相位角的出现,并且角度变化与频率变化相关。
换言之,振幅响应变化伴随着相位响应变化。这些相移是不可避免的,而且是滤波器所固有的。事实上,它们经常可以通过观察振幅响应来预测。当振幅和相位响应以可预测的方式相关时,这种关系称为“最小相位”,并且(有时)是滤波器的理想属性。
因为扬声器的频率响应中的凸起和下降部分通常也是最小相位。这意味着均衡器完全“均衡”扬声器的响应特性,带来更平滑的振幅和相位响应。因此,在这种情况下,“相位偏移”不是使用滤波器的一个有害的副作用,有些人可能也意识到这一点了,因此要“具体问题具体分析”。
澄清一下,“最小相位”并不意味着不存在相移。它是指在特定的振幅响应条件下相对应的相位响应偏移最小,并且可以通过频率响应变化来预测相位响应变化。系统测量程序可以通过给定的振幅响应来计算最小相位响应。
线性相位
FIR滤波器可以在影响振幅响应的同时不影响相位响应。在使用之前的滤波器组的前提下,我用具有相同振幅响应的FIR滤波器代替了高通和低通 IIR滤波器。
这种滤波器的相位响应在频率轴线上是一条直线,因此被称为“线性相位”。请注意,由于高通和低通的相移已被消除,仅留下了振幅提升和衰减产生的相移(图3)。
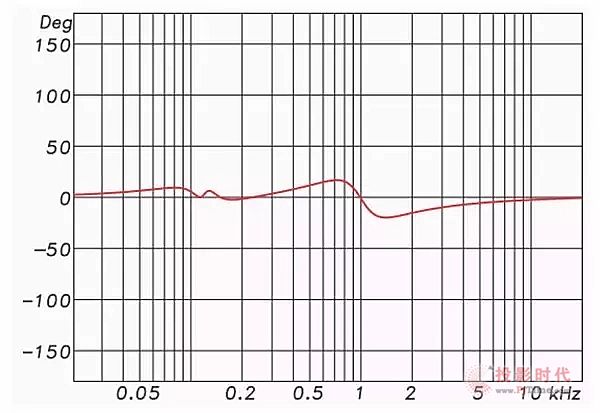
图3:使用FIR滤波器进行高通和低通处理
因此,对于最小相位滤波器来说,振幅和相位响应是相互影响的;而对于FIR滤波器来说,它们可以是独立的。FIR滤波器可以改变振幅响应而不改变相位响应。
从以下开始,我们假设IIR滤波器是最小相位滤波器,FIR滤波器可以是线性相位滤波器。分别使用这两种类型的滤波器产生完全相同的振幅响应曲线,但它们的相位响应曲线可能不同。实际上,如果你只看我举例中的FIR高通和低通滤波器的相位响应曲线,可能根本想不到已经应用了滤波器。
FIR滤波器最大的优势是用于分频网络。用于保护高频驱动器的高通滤波器(HPF)可以使用96 dB/ octave或更高斜率的FIR滤波器。具有这种高斜率的最小相位滤波器(IIR或模拟)的相位响应非常糟糕,因为当其振幅响应曲线效率非常高的时候,其相位响应曲线斜率也会非常高(参考图2)。
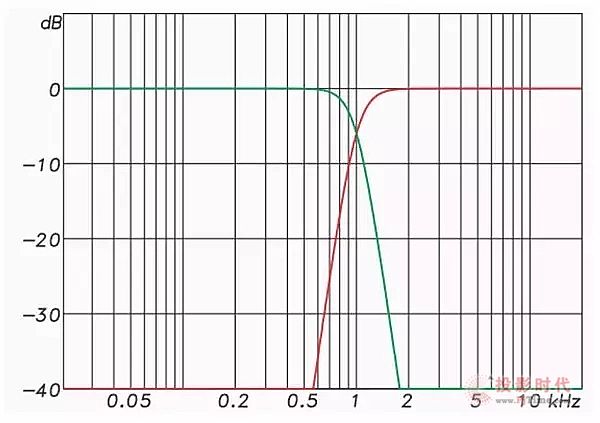
图4:48 dB / oct LR分频网络的频率响应。
这些滤波器叠加以产生完全平坦的幅度响应。
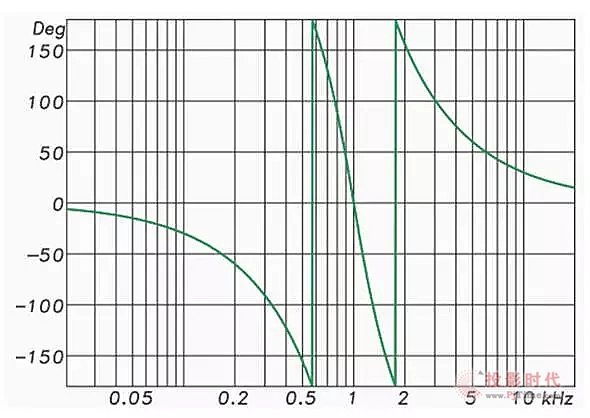
图5:48dB/oct LR分频网络的相位响应(滤波器叠加)
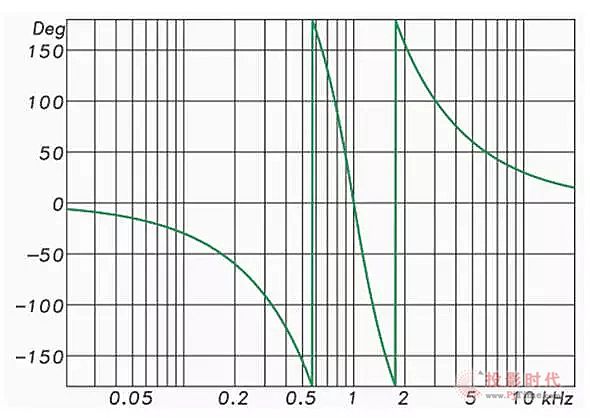
图6:96dB/oct分频网络的频率响应
这些滤波器叠加以产生完全平坦的幅度响应。
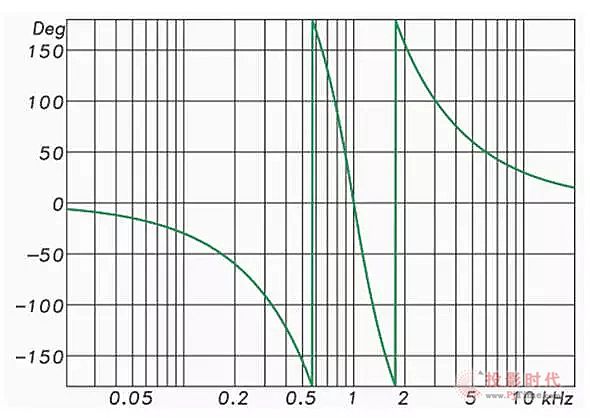
图7:叠加后的分频滤波器的组延时响应。
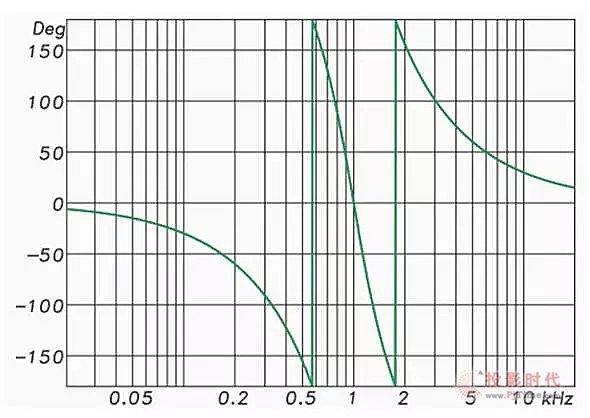
图8:去除组延时的相位响应
IIR分频网络的斜率(阶)有实际的限制,这是由滤波器引起的“时间污染”造成的。
图4和图5显示了一个48 dB / octave Linkwitz-Riley IIR分频网络(HP和LP)的振幅和相位响应。
图6显示了第八阶(96 dB/倍频程)FIR分频网络的振幅响应。请注意,滤波器斜率比IIR示例更陡,通常我们会认为如此剧烈的振幅响应变化会导致相位响应的严重偏移。人们会期望振幅响应的这种积极变化伴随着剧烈的相位响应变化。
图7 显示了滤波器叠加后的组延时(GD)响应曲线,图8显示了去除多余GD后的相位响应。请注意,相位响应是线性的。
使用FIR分频网络,我甚至可以形成“砖墙”衰减特性和线性相位。当然,我需要为线性相位付出一些代价。这对滤波器产生了超过20毫秒的延迟。延迟是我们使用FIR滤波器的顾虑之一。
两种类型
如上所述,音频工作中基本上使用两种类型的滤波器,每种滤波器通常有多个术语描述,它们是:

这些术语存在着明显的自相矛盾。例如,可以在数字域中创建IIR滤波器。FIR滤波器可以是最小相位。然而,这些是两种滤波器类型的“常用用法”标志符,对于常规讨论是很有用的。但在专研细节时,澄清术语非常重要。本文系列中将使用哪些术语?所有这些都会使用,根据上下文决定使用哪些术语。
脉冲响应作为滤波器
那些制作扬声器和房间测量的人都熟悉脉冲响应。尽管可以通过记录系统播放的Dirac脉冲来测量,但各种因素表明这种技术是完全不切实际的。大多数测量系统通过播放对数正弦波扫频信号或“线性调频”信号,捕捉系统响应并处理后获得IR响应。IR可以转换为频域图形(快速傅里叶变换或FFT),并显示为振幅/相位图。振幅/相位图可转换(反向快速傅立叶变换或iFFT)回时域以作为脉冲显示。也就是说,可以从时域或频域方面来描述滤波器的行为特性。如果您通常使用双通道FFT测量平台的话,那么您就已经熟悉这些概念了。
这与FIR滤波器有什么关系?扬声器和房间的脉冲响应是FIR滤波器,由于长度有限,它们会完全衰减到零(或本底噪声)。使用GratisVolver软件来对使用了消声材料的房间脉冲响应(RIR)进行卷积计算的人,实际上就是在使用FIR滤波器(图9)。因此,尽管在实际使用中可能是通过软件或硬件在频域中使用乘积法实现,FIR有时会被称为“时域”或“卷积”滤波器。
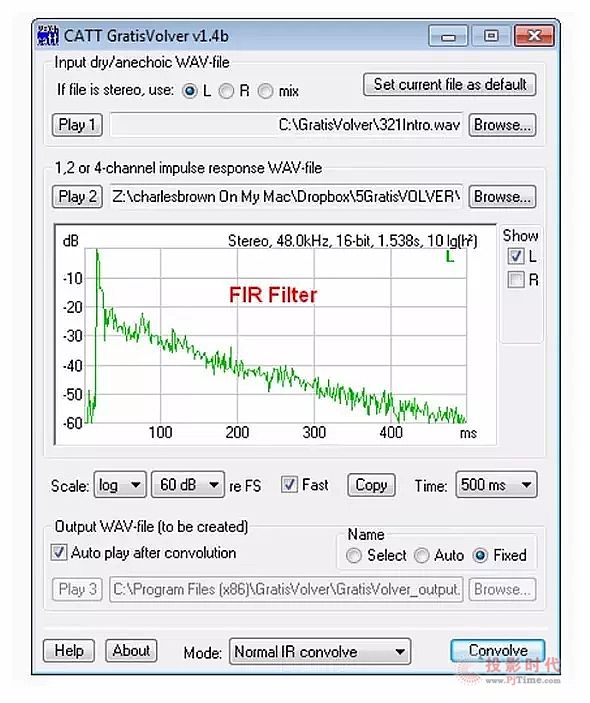
图9:
使用GratisVolver软件对使用消声材料的
房间的脉冲响应(FIR滤波器)进行卷积计算。
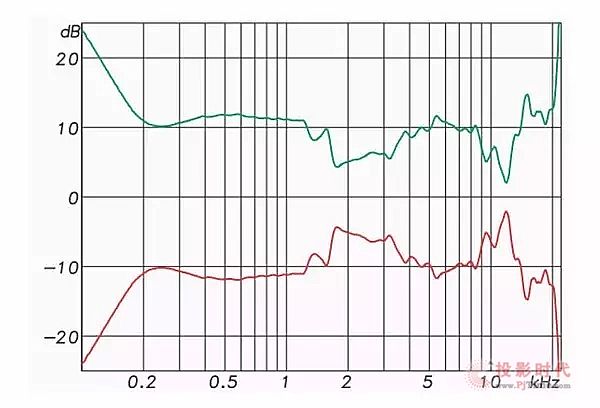
图10:
3英寸扬声器的频响曲线(红色)及其共轭响应(绿色)。如果绿色图形用作均衡滤波器,则结果是完美的响应。(频域中的平坦频响曲线和线性相位,以及时域中的完美脉冲)。
扬声器的IR可以转换为频域图形并显示为频率振幅和相位。 如果在频域中反转IR(上下颠倒),则是扬声器在振幅和相位响应上的精确共轭(相反)(图10)。如果原始和共轭响应相乘,则它们完全相互抵消,产生平坦的幅度和相位响应曲线(频域)或时域中的完美脉冲。
这对均衡工作有很大影响 - 任何测量响应都可以用作滤波器。 FIR“校正”滤波器可用于:
1. 使扬声器的频率响应和相位响应曲线完全平坦,甚至能够补偿由喉管反射,格栅效应和边缘衍射引起的异常。
2. 修正房间异常情况,如扬声器附近的边界效应,以及(理论意义大于实际意义)房间反射。
3. 通过对线性阵列当中的每一个阵列组件进行单独处理来优化线性阵列的响应特性,能够实现模拟滤波器所不能实现的波束成形和波束指向控制。
FIR可以对节目素材进行卷积计算并用作滤波器。虽然这个概念已经存在数十年了,但直到现在才得以实现。许多DSP开始支持FIR滤波器的应用,允许对IR进行实时卷积计算。
但是,在对获得“完美”的扬声器响应特性并消除房间反射感到兴奋之前,我们还需要讨论更多内容。
通过FIR滤波器可以在空间中的某一点获得“完美”的响应特性。但是,由于空间中每个点的IR特性都不一样,所以我们不能将“修正”扩展到一个区域。 这并不意味着FIR均衡是没有用的,只不过是还没有达到完美的听觉体验。我们必须接受在一些特定条件下才能在某些方面受益,并且随着房间面积的增加这些受益的获得也会随之更加困难。
结论
以下是FIR滤波器介绍中的一些实用集锦:
1. FIR可以改变扬声器的振幅响应,而不改变它的相位响应。这个特性允许我们使用斜率非常陡峭的分频滤波器而不会引起相位响应的偏移。获得这种线性相位特性的代价是延时的增加。
2.任何测量获得的脉冲响应都可以用作FIR滤波器。这个特性允许我们对房间测量数据进行“聆听“,例如使用GratisVolver软件或者进行使用模拟滤波器无法实现的均衡优化。这些工作甚至可以在飞行中完成,例如对会议系统进行回声消除优化。
3. FIR可以植入进行卷积计算的软件。例如使用GratisVolver来“聆听”房间脉冲响应。
4. FIR植入硬件设备,用于实时信号处理。现在已经有多个DSP产品支持用户自定义FIR滤波器。
所以在扩声系统领域中,FIR的主要用途是:
1. 分频网络
2. 扬声器均衡校正。
3. 通过卷积计算软件“聆听”房间响应,无论这个响应数据是由房间建模程序生成还是测量所得。
4. 在线性阵列系统中用于波束成形。
音频滤波器不再仅限于电容、电感和电阻的集合,或者通过使用集成电路实现同样功能的等效电路。它们还可以通过测量或数学算法生成,并通过先进的数字信号处理技术实现实时处理。
 L-Acoustics L-ISA助力香港文化中心打造全新沉浸声大剧院作者:佚名 24-07-09
L-Acoustics L-ISA助力香港文化中心打造全新沉浸声大剧院作者:佚名 24-07-09 TWAUDiO助力中国东方演艺集团演出活动作者:佚名 24-07-08
TWAUDiO助力中国东方演艺集团演出活动作者:佚名 24-07-08 德国SAL(声爱乐)联袂众多国际知名音响品牌进驻大庆油田总部作者:佚名 24-07-03
德国SAL(声爱乐)联袂众多国际知名音响品牌进驻大庆油田总部作者:佚名 24-07-03 Biamp发布用于大型空间语音扩声系统的Community R.15-3696扬声器作者:佚名 24-07-02
Biamp发布用于大型空间语音扩声系统的Community R.15-3696扬声器作者:佚名 24-07-02 创新专利声学设计,世邦智能均衡音箱如何实现声学突破?作者:佚名 24-06-28
创新专利声学设计,世邦智能均衡音箱如何实现声学突破?作者:佚名 24-06-28 音符跃动,绿意盎然 —— Meye迈雅音响点亮绿之声音乐会馆音乐之旅作者:佚名 24-06-28
音符跃动,绿意盎然 —— Meye迈雅音响点亮绿之声音乐会馆音乐之旅作者:佚名 24-06-28 VCV Rack Spectra 16 段频谱处理器作者:pjtime资讯组 18-08-09
VCV Rack Spectra 16 段频谱处理器作者:pjtime资讯组 18-08-09 内含环状滤波器:Cardas Clear M电源线作者:pjtime资讯组 18-05-17
内含环状滤波器:Cardas Clear M电源线作者:pjtime资讯组 18-05-17 提升电源纯度:美国音乐丝带Nordost Quantum QK1作者:pjtime资讯组 16-11-22
提升电源纯度:美国音乐丝带Nordost Quantum QK1作者:pjtime资讯组 16-11-22 PAL网络数字扩声系统亮相2016专业音响展作者:佚名 16-03-18
PAL网络数字扩声系统亮相2016专业音响展作者:佚名 16-03-18 Stein Music给你更纯的讯号:Speaker Match Plus喇叭线滤波器作者:pjtime资讯组 15-11-23
Stein Music给你更纯的讯号:Speaker Match Plus喇叭线滤波器作者:pjtime资讯组 15-11-23 商用/家用皆可行:Tripp Lite HT10DBS电源讯号滤波器作者:pjtime资讯组 14-01-03
商用/家用皆可行:Tripp Lite HT10DBS电源讯号滤波器作者:pjtime资讯组 14-01-03